清华大学航院陈常青课题组在非保守拓扑力学领域取得新进展
2024/04/09
676自然界和人工系统的演化往往是非保守的，伴随着与外部环境间的能量交换。例如，运动的物体会因为空气阻力而损失动能，冰在融化时会不断吸收外部热量等。这些非保守的动力学演化过程可以用一类特殊的算符—非厄米哈密顿量进行刻画。当系统的微组织结构是规则周期时，它的宏观属性在很大程度上取决于周期结构的能带特性。如果将非厄米与拓扑能带巧妙结合，则有可能在拓扑绝缘体、拓扑声学和拓扑力学等系统中催生出奇异点、宇称-时间对称性及非厄米趋肤效应等一系列新奇的拓扑现象，在能量收集、信息传输、认知型材料等方面具有广泛的应用前景。
但一个广为接受的共识是，与外界保持持续能量交换的开放系统是研究非厄米拓扑行为的一个不可或缺的条件，而构建具有拓扑效应的非保守动态系统，无论是在宏观的力学、电磁、声学系统和生物群落，还是微观的量子系统，都并非易事。如能在静态的保守系统中实现非厄米拓扑行为，将会为非厄米拓扑力学和物理研究带来巨大方便。
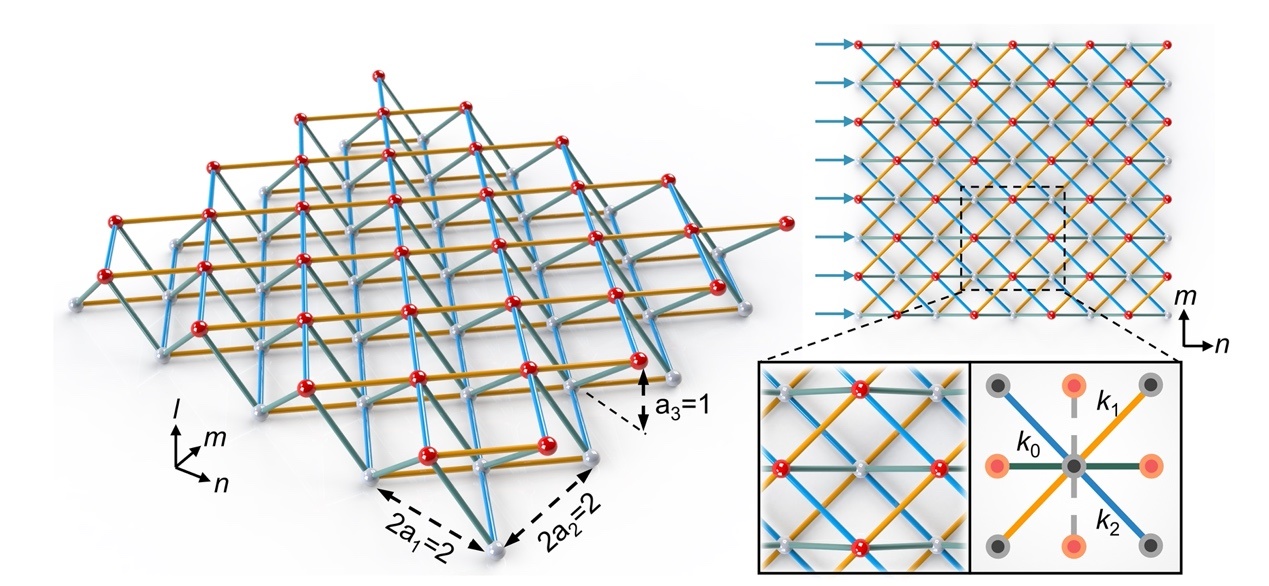
图1.静态力学超材料模型
最近，清华大学航天航空学院陈常青教授课题组利用力学超材料点阵结构，将低维非保守系统中的弹性波时域动力学演化行为，等效映射为空间尺度上高维点阵结构的静态变形模式，从而在一个静态的保守系统中实现了非厄米拓扑效应（图1）。相较于非厄米动力学系统，该静态系统中仅通过改变点阵的几何构型便能实现非厄米及等效非互易效应，而无需任何主动调控或能量注入，极大地降低了非厄米效应的触发条件（图2）。
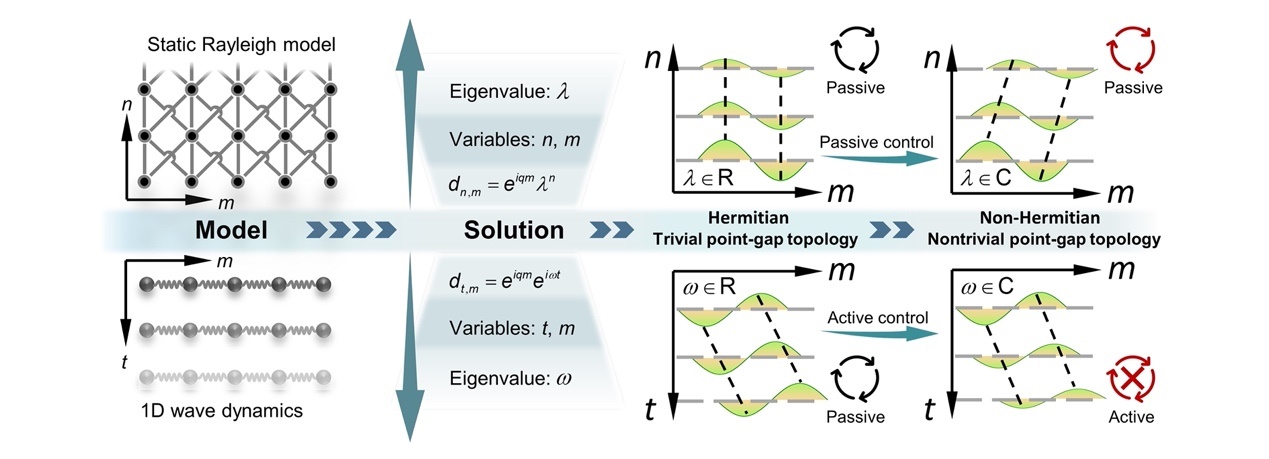
图2.一维动力学系统与二维静力学系统间的等价映射关系
借助于非厄米拓扑能带理论，陈常青课题组在静态系统中实现了多种非厄米拓扑效应，包括趋肤效应诱导的本征态非对称分布、拓扑零能模式的非厄米重构以及高阶趋肤效应等。不同于波动力学，非厄米拓扑静力学可以用来表征点阵结构的空间变形分布，比如调控静态变形传输路径（图3），或者设计具有自适应变形屏蔽功能的超材料。上述变形信息的可定制高效传输是机械计算的关键，也是实现具有信息感知、编码、存储、计算、决策等信息处理能力的认知型力学超材料的基础。
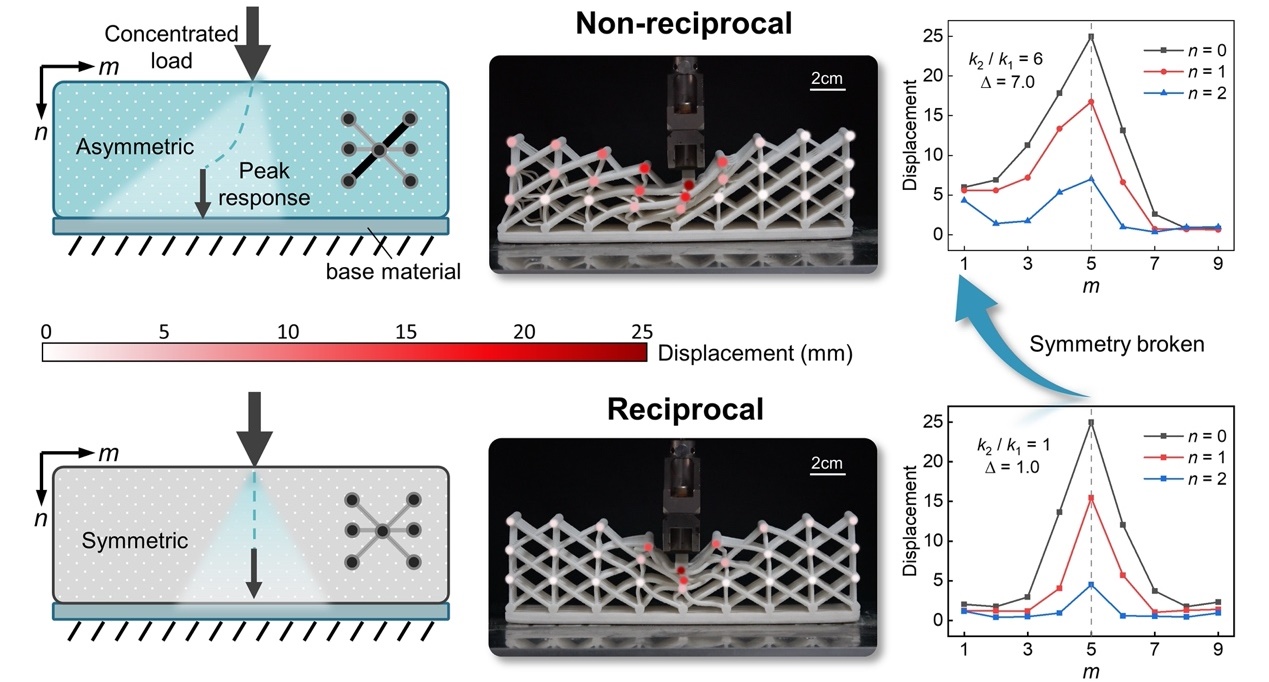
图3.静态变形路径调控
相关研究成果以“静态力学超材料中的非厄米拓扑”（Non-Hermitian topology in static mechanical metamaterials）为题，近日在《科学·进展》（Science Advances）发表，并入选当期的“特别推荐文章”（FeaturedImage Articles）（图4），展示出静态保守系统的非厄米拓扑行为及应用，也为量子及经典波动系统中非厄米拓扑理论的深入研究提供了全新的平台。
图4.入选当期的“特别推荐文章”
清华大学航天航空学院陈常青教授为论文通讯作者，2021级博士生王澳西为第一作者。作者还包括2018级博士生孟志强。该研究得到国家自然科学基金委重点项目和创新群体项目的支持。近年来，陈常青课题组在力学超材料领域取得了一系列成果，包括拓扑静态孤子、多路径变形力学超材料以及具有信息的机械计算、编码和存储等信息处理能力的自认知力学超材料等。
鏂囩珷鏉ユ簮清华大学新闻锛屽垎浜彧涓哄鏈氦娴侊紝濡傛秹鍙婁镜鏉冮棶棰樿鑱旂郴鎴戜滑锛屾垜浠皢鍙婃椂淇敼鎴栧垹闄ゃ
-
2026骞寸鍏眾璁＄畻鏈虹瀛︿笌鎶鏈湪鏁 109
-
2026骞3鏈堥珮鍚噾閲忓浗闄呭鏈細璁悎 88
-
2026璧勬簮銆佸寲瀛﹀寲宸ヤ笌搴旂敤鏉愭枡鍥介檯 1265
-
2026骞翠汉宸ユ櫤鑳芥暀鑲叉妧鏈笌鏁版嵁绉戝 246
-
2026骞村浘鍍忓鐞嗕笌鏁板瓧鍒涙剰璁捐鍥介檯 1041
-
2026骞存満姊板伐绋嬶紝鏂拌兘婧愪笌鐢垫皵鎶鏈 5524
-
2026骞存潗鏂欑瀛︺佷綆纰虫妧鏈笌鍔ㄥ姏宸 1312
-
2026骞寸浜屽眾鏃犵嚎涓庡厜閫氫俊鍥介檯浼氳 2080
-
绗竷灞婂缁勫绉戠爺涓庝复搴婂簲鐢ㄥぇ浼 02-05
-
2026骞村埗鑽銆佺敓鐗╂妧鏈笌妞嶇墿瀛﹀浗 02-04
-
2026骞磋妭鑳芥妧鏈佷綆纰冲彂灞曚笌鍙寔缁 02-04
-
2026骞村鑸帶鍒躲佷紶鎰熸妧鏈笌鍗槦搴 02-04
-
2026骞寸粡娴庤浆鍨嬩笌鍟嗕笟鏂囧寲鍥介檯瀛︽湳 02-04
-
2026骞翠綋鑲茬瀛︺佽繍鍔ㄥ仴搴蜂笌鍒涙柊绠 02-04
-
2026鍒涙剰鍩庡競銆佽璁′笌绀惧尯寤鸿鍥介檯 02-04
2026骞翠綆绌虹粡娴庝笌鎶鏈簲鐢ㄥ浗闄呭鏈細璁 (.
2026骞寸浜屽眾鏃犵嚎涓庡厜閫氫俊鍥介檯浼氳(CWO.
2026骞寸浜斿眾浜氭床绠楁硶銆佽绠椾笌鏈哄櫒瀛︿範鍥介檯.
绗叚灞婄墿鑱旂綉涓庢櫤鎱у煄甯傚浗闄呭鏈細璁紙IoTS.
2026骞寸浜斿眾浜戣绠椼佽绠楁満瑙嗚鍜屽浘鍍忓鐞.
绗簩灞婄幆澧冪洃娴嬩笌鐢熸佷慨澶嶅浗闄呭鏈細璁紙EME.
绗叚灞婅兘婧愬伐绋嬨佹柊鑳芥簮鏉愭枡涓庡櫒浠跺浗闄呭鏈細璁.
绗簩灞婁汉宸ユ櫤鑳姐佽櫄鎷熺幇瀹炰笌浜や簰璁捐鍥介檯瀛︽湳浼.
绗叚灞婂簲鐢ㄦ暟瀛︺佸缓妯′笌鏅鸿兘璁＄畻鍥介檯瀛︽湳浼氳锛.
绗簩灞婃ˉ闅у缓璁句笌宸ョ▼鍥介檯瀛︽湳浼氳锛圔TCE .
绗叚灞婂浘鍍忓鐞嗕笌鏅鸿兘鎺у埗鍥介檯瀛︽湳浼氳锛圛PI.
2026骞寸鍏眾璁＄畻鏈哄浘褰㈠銆佸浘鍍忎笌鍙鍖栧浗.
绗崄涓夊眾鍏堣繘鍒堕犳妧鏈笌鏉愭枡宸ョ▼鍥介檯瀛︽湳浼氳 .
2026 骞寸涓夊眾璁＄畻锛屾満鍣ㄥ涔犱笌鏁版嵁绉戝鍥.
绗叚灞婅嚜鍔ㄥ寲鎺у埗銆佺畻娉曚笌鏅鸿兘浠跨敓鍥介檯瀛︽湳浼氳.
2026骞寸鍥涘眾浜氭床璁＄畻鏈鸿瑙夈佸浘鍍忓鐞嗕笌妯.
2026骞寸浜斿眾缃戠粶銆侀氫俊涓庝俊鎭妧鏈浗闄呬細璁.
-
2025骞翠袱闄㈤櫌澹閫夋湁鏁堝欓変汉4066
-
2025鏈鏂癑CR鍒嗗尯鍙婂奖鍝嶅洜瀛10070
-
濂藉鏈:绉戠爺缃戝潃瀵艰埅|瀛︽湳澶存潯鍒5098
-
2025骞村浗闄呮湡鍒婇璀﹀悕鍗曞彂甯!5129
-
2025骞翠腑绉戦櫌鏈熷垔鍒嗗尯琛ㄩ噸纾呭彂16711
-
涓浗绉戝崗銆婇噸瑕佸鏈細璁洰褰曪紙2010250
-
鍚夋灄澶у鏍￠暱寮犲笇锛氬鏈細璁腑鐨勬彁6245
-
bbrc鏈熷垔,bbrc鏈熷垔澶勪簬S02-03
-
siam鏈熷垔,siam鏈熷垔鍙戠殑鏈02-03
-
浜嗘湜鏈熷垔,鐬湜鏈熷垔02-03
-
鍏变韩缁忔祹鏈熷垔,鍏变韩缁忔祹瀛︽湳璁烘枃02-03
-
鏈熷垔浠ｇ悊缃,浠庡摢閲屾壘鏈熷垔浠ｇ悊02-03
-
light鏈熷垔,Light鏈熷垔缁02-03
-
浼犳壙 鏈熷垔,浼犳壙鏈熷垔鎶曠ǹ鐐硅瘎02-03
-
鏈熷垔鍕樿,鏈熷垔鍕樿鏃朵細绱㈣鍘熷鏁02-03
-
IAASE 8216
-
湖南长沙市碧桂园凤凰酒店(原威尼 23162
-
guizhoushifandax 23225
-
深圳市安视佳电子监控摄像机厂家 18276
-
北京金奖杯工艺品有限公司 21223
-
上海广贸会展服务有限公司 23450
-
工程信息研究院 18241
-
Focussend 24381
-
上海第二工业大学 2210
-
复旦大学 18265
-
APISE 23265
-
解放军总医院第一附属医院超声科 21365
-
中国农科院植保所 21242
-
中昊科隆展览有限公司 8226
-
中国科学院武汉岩土力研究所 2138
-
兰州泛海佳乙广告有限公司 18175
-
武汉青博盛学术服务有限公司 23284
-
qs 24208
-
IWMH会务组 21426
-
河北北方大厦 21292
