清华大学数学中心张景宣合作在量子多体动力学研究中取得进展
2025/10/20
83过去几十年中，量子多体物理研究取得了卓越成就，特别是对于近平衡态和相互作用较弱的情形，目前已经形成比较完善的理论框架。然而，前沿量子应用中常常需要考虑量子多体系统远离平衡态时的动力学过程。例如，对一个在极小空间中集成了大量量子比特的量子器材进行精准调控，在理论层面需要处理强关联多粒子系统中的非平衡动力学问题。这类问题无法用绝热近似、平均场近似等传统解析方法处理，且在高维情形下极难进行精确的数值模拟，当前已经成为量子物理领域最具有挑战性的课题之一。
近日，清华大学数学科学中心博士后张景宣与合作者运用一种称为“几何指数加权”的新数学方法，在量子多体动力学研究中取得重要进展。研究团队聚焦强关联多粒子系统的动力学行为，证明了宏观粒子团簇的输运受到与系统总粒子数相关的严格制约，揭示了非平衡量子多体系统中一种普适性的物理规律。
在非平衡量子多体系统中，物理效应会通过粒子之间的相互作用在系统中传播。1972年，埃利奥特·利布（Elliott Lieb）与德雷克·罗宾逊（Derek Robinson）首次证明了量子自旋系统中，物理效应的最大传播速率存在一定界限。在粒子间相互作用的制约下，超过这一界限的传播都会受到抑制。这一界限远低于狭义相对论给出的光速界限，被物理学家普遍称为“音速”。2012年，马克·切瑙（Marc Cheneau）团队在光晶格实验中，验证了利布-罗宾逊界限，相关成果发表于《自然》杂志第481期。
张景宣与合作者发现了一种针对“超音速”量子输运的宏观抑制机制。这种机制对于一般量子多体系统都成立，并且对于“超音速”输运行为的抑制强度与系统内总粒子数成指数相关。结合一维光晶格实验中的实际情况，理论计算表明，对于由18个粒子组成、相邻格点之间距离为500nm、跳跃幅度为500s-1的玻色-哈伯德（Bose-Hubbard）模型，在6.67×10-4s的观测时间内发生跨越6个格点以上的“超音速”输运的概率上界为1.52×10-18，比传统理论给出的概率上界0.37精确超过17个数量级。这一结论说明，在大尺度上，无论是玻色子还是费米子体系，即便是在长程强相互作用下，“超音速”量子输运都会受到显著抑制，因此几乎不可能在宏观层面被观测到。
研究团队提出一种几何变形方法，通过为不同传播区域赋予适当指数权重，将宏观输运问题转化为对变形后的幺正演化算子的范数估计，结合哈密顿量的衰减性质和二次量子化工具，最终得到“超音速”输运的概率上界。这是研究人员首次在量子多体系统中发现与总粒子数相关的“超音速”输运抑制机制，为进一步理解现实量子应用中强关联多粒子系统的动力学行为提供了重要理论支撑。
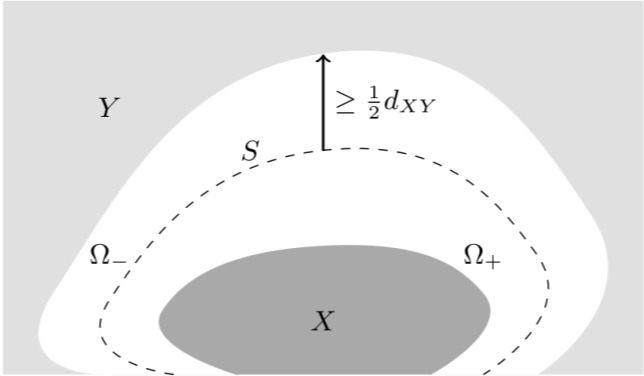
几何变形对应区域示意图
研究成果以“超音速量子输运的宏观抑制”（Macroscopic suppression of supersonic quantum transport）为题，于10月16日发表于《物理评论快报》（Physical Review Letters）。
清华大学数学科学中心博士后张景宣为论文共同通讯作者。其他合作者包括法国洛林大学教授杰瑞米·法奥庞（Jérémy Faupin），德国蒂宾根大学教授马里乌斯·兰姆（Marius Lemm），以及加拿大皇家学会院士、多伦多大学教授伊斯雷尔·迈克尔·西格尔（Israel Michael Sigal）。研究得到国家重点研发计划、国家自然科学基金、博士后科学基金等的资助。
鏂囩珷鏉ユ簮清华大学锛屽垎浜彧涓哄鏈氦娴侊紝濡傛秹鍙婁镜鏉冮棶棰樿鑱旂郴鎴戜滑锛屾垜浠皢鍙婃椂淇敼鎴栧垹闄ゃ
-
2026骞1鏈堥珮鍚噾閲忓浗闄呭鏈細璁悎 12-12
-
绗洓灞婇噾铻嶇鎶涓庡晢涓氬垎鏋愬浗闄呭鏈細璁 686
-
2026骞寸鍗佷竴灞婂鍚堟潗鏂欎笌鏉愭枡宸ョ▼ 1453
-
2025骞存満鍣ㄨ瑙夈佹櫤鑳芥垚鍍忎笌妯″紡璇 2126
-
2025骞存櫤鑳藉厜瀛愬涓庡簲鐢ㄦ妧鏈浗闄呭 3284
-
2026骞存満姊板伐绋嬶紝鏂拌兘婧愪笌鐢垫皵鎶鏈 3476
-
2025骞磋绠楁満绉戝銆佸浘鍍忓垎鏋愪笌淇″彿 3917
-
2025骞存潗鏂欏寲瀛︿笌鐕冩枡鐢垫睜鎶鏈浗闄 3633
-
2026骞翠氦閫氭暟瀛楀寲銆佷汉宸ユ櫤鑳戒笌闊ф 12-19
-
2026骞寸ぞ浼氭枃鍖栦笌鍏叡绠＄悊鍥介檯浼氳 12-19
-
2026骞翠汉鏂囧湴鐞嗕笌璇█鐮旂┒鍥介檯浼氳 12-19
-
2026骞寸ぞ浼氬彂灞曚笌缁忔祹鍙戝睍鍥介檯浼氳 12-19
-
2026骞村厜浼忔潗鏂欍佸厜鐢佃浆鎹笌鍙啀鐢 12-19
-
2026骞村彲鎸佺画鍙戝睍涓庢暟瀛楀寲绀句細鍥介檯 12-19
-
2026骞寸鐞嗙瀛︺佽瑷涓庢暀鑲插浗闄呬細 12-19
绗簩灞婄數鍔涚數瀛愭妧鏈笌鐢电綉绯荤粺鍥介檯瀛︽湳浼氳锛圥.
2026鎷撳睍鐜板疄銆佷汉鏈轰氦浜掍笌浜哄伐鏅鸿兘鍥介檯鐮旇.
2026骞存柊涓浠ｆ櫤鑳介氫俊涓庝俊鍙峰鐞嗙爺璁ㄤ細锛圢.
绗簲灞婄數瀛愪俊鎭伐绋嬩笌鏁版嵁澶勭悊鍥介檯瀛︽湳浼氳锛圗.
绗竷灞婃柊鏉愭枡涓庢竻娲佽兘婧愬浗闄呭鏈細璁紙ICAM.
绗簩灞婁汉宸ユ櫤鑳姐佹暟瀛楀獟浣撴妧鏈笌绀句細璁＄畻鍥介檯瀛.
绗簩灞婄數姘斿伐绋嬩笌鏅鸿兘绯荤粺鍥介檯瀛︽湳浼氳锛圛C2.
绗洓灞婇氫俊缃戠粶涓庢満鍣ㄥ涔犲浗闄呭鏈細璁(CNM.
绗簲灞婅兘婧愬埄鐢ㄤ笌鑷姩鍖栧浗闄呭鏈細璁紙ICEU.
绗簩灞婁华鍣ㄤ华琛ㄤ笌瀵艰埅鎺у埗鍥介檯瀛︽湳鐮旇浼 (I.
2026骞寸浜屽眾鏃犵嚎涓庡厜閫氫俊鍥介檯浼氳(CWO.
2026骞寸浜斿眾浜氭床绠楁硶銆佽绠椾笌鏈哄櫒瀛︿範鍥介檯.
2026骞寸浜斿眾浜戣绠椼佽绠楁満瑙嗚鍜屽浘鍍忓鐞.
2026骞寸鍏眾璁＄畻鏈哄浘褰㈠銆佸浘鍍忎笌鍙鍖栧浗.
-
2025骞翠袱闄㈤櫌澹閫夋湁鏁堝欓変汉2672
-
2025鏈鏂癑CR鍒嗗尯鍙婂奖鍝嶅洜瀛7552
-
濂藉鏈:绉戠爺缃戝潃瀵艰埅|瀛︽湳澶存潯鍒3540
-
2025骞村浗闄呮湡鍒婇璀﹀悕鍗曞彂甯!3510
-
2025骞翠腑绉戦櫌鏈熷垔鍒嗗尯琛ㄩ噸纾呭彂13412
-
涓浗绉戝崗銆婇噸瑕佸鏈細璁洰褰曪紙207866
-
鍚夋灄澶у鏍￠暱寮犲笇锛氬鏈細璁腑鐨勬彁4517
-
涓浗绉戝ぇ鎻愬嚭鈥嬬數鍖栧涓浣撳寲椹卞姩绛12-19
-
涓浗绉戝ぇ瀹炵幇鐢垫车娴︾墖涓婇泦鎴愰珮浜害12-19
-
瑗垮寳鍐滄灄绉戞妧澶у銆愰檿瑗挎柊闂昏仈鎾12-19
-
涓浗绉戝ぇ瀹炵幇鐗囦笂闈炵浉骞叉车娴﹂珮鍝佽川12-19
-
涓浗绉戝ぇ涓у師瀛愰噺瀛愯绠楃爺绌舵垚鏋12-19
-
鐐旂儍杩滅C-O閿殑涓嶅绉版椿鍖栬浆鍖12-19
-
鐮旂┒鎻ず鍙剁墖鍐呯敓鐪熻弻鍒嗗瓙鍔熻兘澶氭牱12-19
-
绉戠爺浜哄憳鎻愬嚭鏌戞榛勯緳鐥呴槻鎺ф柊绛栫暐12-19
-
北京学苑新报 18279
-
江西省南昌市洪都中学 18327
-
百奥泰国际会议（大连）有限公司 24010
-
East Asia Resear 21273
-
南昌大学 21306
-
2018年信息科学与技术国际会议 21094
-
Hong Kong Indust 18207
-
北京科爱森蓝文化传播有限公司 8335
-
国际工学技术出版协会 8159
-
中华医学会眼科学分会 18658
-
北京市丰台区 18173
-
黄山梅地亚酒店 18181
-
延边大学 2142
-
百奥泰国际会议（大连）有限公司 23216
-
上海万怡会展管理股份有限公司 8123
-
中国食品药品企业质量安全促进会消 8089
-
HKSME 23199
-
上海同济大学 18428
-
陕西汉中供电局 21404
-
番禺理工学院 18154
