南京大学物理学院声学研究所、近代声学教育部重点实验室、人工微结构科学与技术协同创新中心梁彬和程建春课题组在声波的自旋-轨道耦合方面取得重要进展，首次发现了涡旋声束可以携带非零的纵向自旋角动量，并基于此揭示了声波的全局自旋-轨道耦合机制。

自旋和轨道角动量是波动物理中的重要概念，已在光学等横波系统中得到深入研究并广泛应用于光学信息处理和精密测量等领域。相比之下，声波在流体中传播时表现为纵波，因此按照传统观点，声波似乎不可能携带类似“自旋”的自由度，对声角动量的研究当前也主要集中在轨道角动量层面。尽管近年来的研究发现声场中可以存在非零的局域自旋密度，但这种局域自旋在自由空间的全局积分中会相互抵消，导致声束的总自旋角动量为零，因此声学系统通常被认为缺乏“全局自旋角动量”这一自由度，难以实现全局自旋-轨道耦合效应。

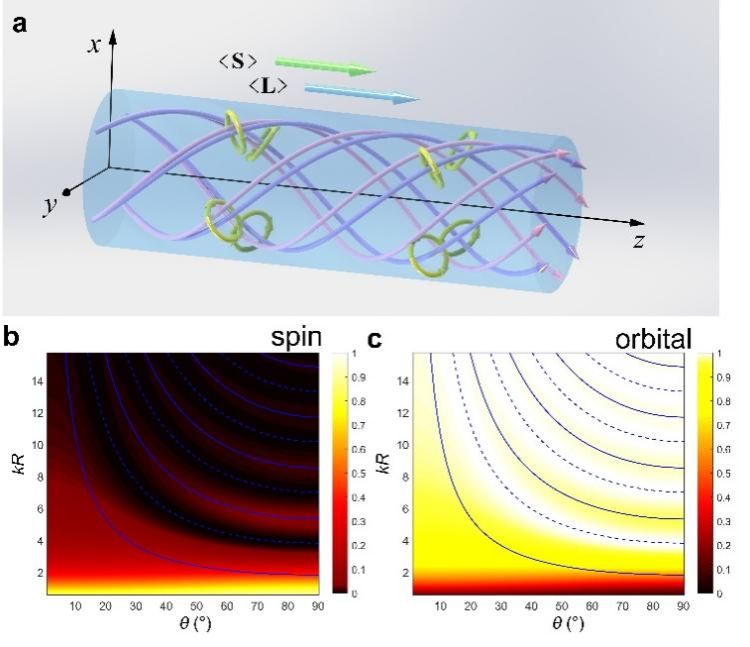
图1：(a)圆柱波导模态的自旋与轨道角动量示意图； (b)(c)：当涡旋的量子数 l=+1时，归一化自旋与轨道角动量随近轴程度及波导半径的变化。

课题组首次提出了在有界系统中构建全局声自旋角动量的机制，通过发展一种自洽的类量子理论框架，并引入同时包含声压和速度场的四分量波函数，对柱状波导中非耗散声场的自旋与轨道角动量进行了系统的理论分析，发现了这类声场可以在特定条件下携带非零的积分纵向自旋角动量，并揭示了其大小与边界处的Abraham动量密度间的量化关系（图1）。对于支持非耗散涡旋声传播的全部边界条件：绝对硬边界、绝对软边界和一般纯抗边界，课题组从声速度场极化椭圆分布的视角阐明了不同边界条件下积分自旋角动量大小与局部声场极化方向的关系（图2）。在绝对硬边界条件下，声场的极化均沿同一方向，此时自旋角动量最大；反之，在绝对软边界条件下，正负方向的极化相互抵消，自旋角动量始终为零；而一般纯抗边界时，极化情况则介于上述两者之间，因此自旋角动量也介于0和最大值之间。

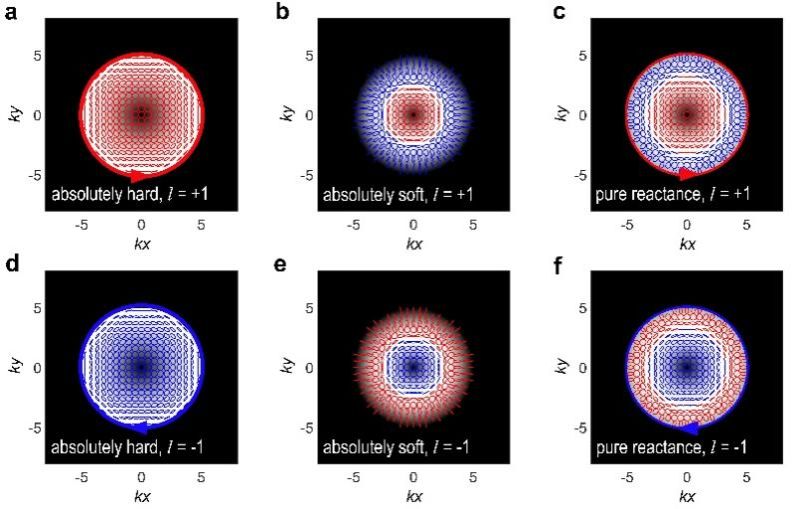
图2：在不同边界条件和不同拓扑荷数时，波导中涡旋声场横截面的声压幅值（灰度背景）分布及速度场 (vx,vy)的极化椭圆。(a) 绝对硬边界，l=+1；(b) 绝对软边界，l=+1；(c) 纯抗边界，l=+1；(d) 绝对硬边界，l=−1；(e) 绝对软边界，l=−1；(f) 纯抗边界，l=−1。波导的无量纲半径为 kR=5。红色和蓝色分别对应右旋（Sz>0）和左旋（Sz<0）的椭圆极化。边界处粗红、蓝箭头的方向和粗细分别表示边界Abraham动量密度的方向和大小。

基于以上理论，课题组进一步提出了声波自旋与轨道角动量的定量调控策略。通过合理设置支持非耗散涡旋态传播的波导系统的边界条件和结构参数，实现了对声波自旋与轨道角动量的精确调控（图3）。此外，课题组还对声学系统中Abraham与Minkowski两种角动量定义进行了分析比较，发现了Minkowski 角动量始终守恒，使得在流体声学中实现全局自旋-轨道耦合成为可能。为了实现对该效应的实验观测，课题组提出了一种通过改变声束傍轴性来调控耦合强度的自旋-轨道耦合机制，并构建了对应的实验验证系统。仅需在缓变截面波导管中激发相应的涡旋模态，并在沿声束传播过程的不同横截面进行积分自旋和角动量的测量，即可实验观测到自旋角动量逐渐向轨道角动量转化的过程，从而严格验证了所提出的自旋-轨道耦合机制（图4）。

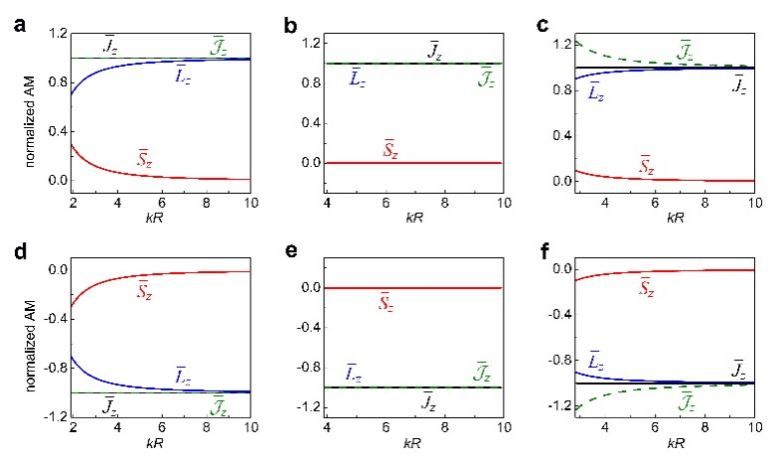
图3：在不同边界条件的柱状波导中，具有不同拓扑荷数的声场的Minkowski自旋、轨道及总角动量和Abraham总角动量随波导半径变化的趋势。(a) l=+1，绝对硬边界；(b) l=+1，绝对软边界；(c) l=+1，纯抗边界；(d) l=−1，绝对硬边界；(e) l=−1，绝对软边界；(f) l=−1，纯抗边界。

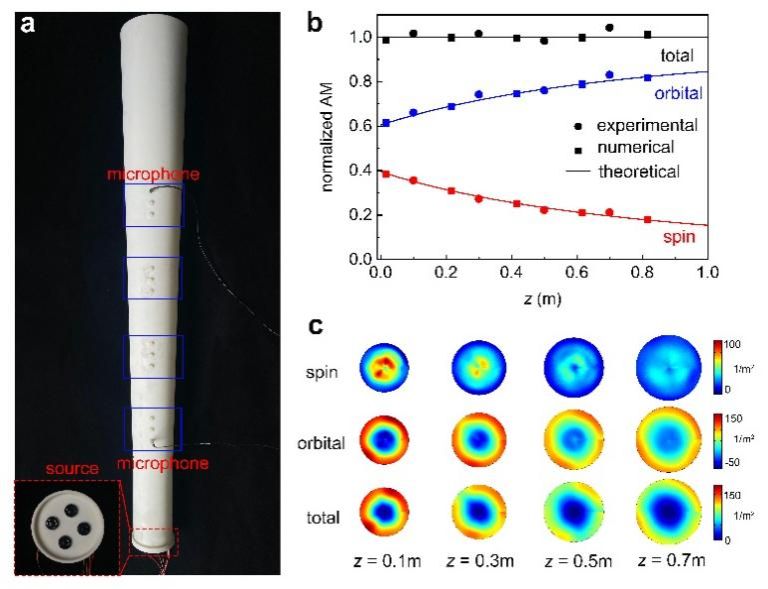
图4：(a) 用于观测全局自旋-轨道耦合效应的实验系统；(b)归一化的Minkowski自旋、轨道及总角动量随传播距离的变化关系曲线，其中实线、方形和圆形分别代表理论、数值和实验结果；(c)不同截面上自旋和轨道角动量密度分布的实验测量值。

该研究揭示了声学中自旋与轨道角动量的本质及两者间的相互作用，为理解经典波体系中的自旋角动量等动力学特性提供了新的视角，也为水下通信和粒子操控等应用开辟了新的可能。相关成果以”Longitudinal acoustic spin and global spin–orbit interaction in vortex beams”为题发表于物理学著名期刊Reports on Progress in Physics [DOI:10.1088/1361-6633/ae15bc]。南京大学物理学院为第一单位，已毕业的王未博士和谭杨博士为共同第一作者，刘京京助理教授、梁彬教授、程建春教授和中国科学技术大学的蒋建华教授为论文的共同通讯作者。该工作得到国家重点研发计划、国家自然科学基金、江苏省自然科学基金、中国科协青年人才托举工程等项目资助。