长安大学方勇教授在分布式信源编码研究方面取得进展
2024/04/18
896 |
图1 传统信源编码和分布式信源编码原理对比示意图：（A）传统信源编码（对称式）；（B）分布式信源编码（对称式）；（C）传统信源编码（非对称）；（D）分布式信源编码（非对称）
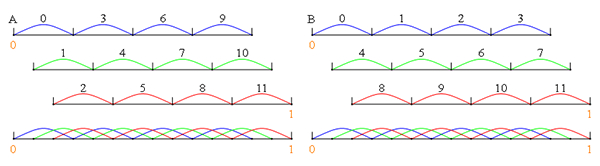
图2 多元分布式算术码的符号-区间映射规则示意图：（A）等距递增；（B）等距交错
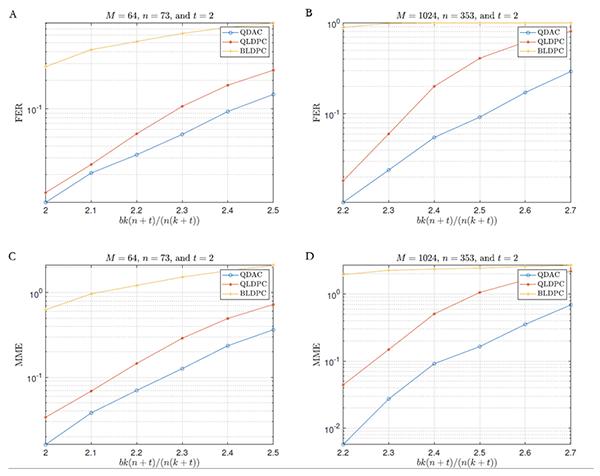
图3 1/2码率下不同码长多元分布式算术码与基于信道码（LDPC码）的分布式信源编码性能对比图（短码码长为75个256元符号，等效于600个比特；长码码长为355个256元符号，等效于2840个比特）：（A）短码误帧率；（B）长码误帧率；（C）短码曼哈顿残差；（D）长码曼哈顿残差
在国家自然科学基金项目（批准号：62141101）资助下，长安大学方勇教授在分布式信源编码研究方面取得进展。研究成果以“多元等概信源的多元分布式算术码（Q-ary Distributed Arithmetic Coding for Uniform Q-ary Sources）”为题于2022年12月 22日发表在期刊《电气电子工程师协会·信息论汇刊》（IEEE Transactions on Information Theory）上。文章链接：https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9944690。源码链接：https://github.com/fy79/Qary-DAC。
近年来，语音、图像、视频等各类数据呈爆炸式增长，为了消除这些数据的冗余度以提高通信有效性，信源编码技术根据信源符号序列的统计特性将其变换为尽可能短的码字序列，使编码后各码元所载荷的平均信息量最大，同时又能无失真（或以尽可能小的失真）来恢复原始符号序列。传统的集中式信源编码主要建立在单信源-单信宿的点到点信息论基础之上，致力于建立单个节点信源编码的率失真理论边界，以及探索可达到这些理论边界的实际编码方案。而在多个节点并存的智能交通稠密监控系统和居民基因数据库等实际应用场景中，多个节点的原始数据中具有很高的时空相关性，如果仍采用传统的集中式信源编码，各节点的信源编码器之间需通过互相通信来获取彼此的信息，存在编码器复杂度高、设备功耗大、布置成本高等问题。与传统的集中式编码方法相比，分布式信源编码方法能够对信息互相关联的多个节点进行独立的信源编码，而不需要节点之间的相互通信，进而在解码端以联合解码的方式恢复出多个节点的原始数据，将计算复杂度由编码端转移到解码端（服务器），从而很好地解决了传统集中式信源编码方法存在的问题（图1）。
由于相关信源之间的预测残差可以建模为虚拟信道的加性噪声，分布式信源编码在本质上等效于虚拟信道上的信道编码问题，因此现有分布式信源编码的实现方式通常基于各种信道码（如Turbo码、LDPC码和极化码）。基于信道码的分布式信源编码实现方式存在的主要问题在于模型失准：信道码通常基于加性白高斯噪声（AWGN）信道模型进行优化，因而在欧式距离的意义上是最优的；然而对于实际相关信源（例如视频信号）而言，其预测残差往往服从拉普拉斯分布，而不是高斯分布。此时，欧氏距离意义上的最优信道码无法同时满足曼哈顿距离意义上的最优，因此基于信道码的分布式信源编码实现方式无法达到Slepian-Wolf定理所给出的无损分布式信源编码的理论极限。
为了缩小现有基于信道码的分布式信源编码实现方式的实际性能与Slepian-Wolf定理的理论极限之间的差距，方勇教授研究了多元分布式算术码，其主要创新性思路在于直接以曼哈顿距离作为度量工具，设计了曼哈顿距离意义上的最优编解码方案。他从理论上严格证明了：随着分组长度趋于无穷大，每个分组的多元分布式算术码流的总码率损失趋于一个有限常数，因此单个符号的平均码率损失趋于零，亦即多元分布式算术码性能可以达到理论极限。多元分布式算术码的设计核心是符号-区间映射规则，为此他提出等距交错符号-区间映射规则（图2），根据曼哈顿距离进行陪集空间分割，解决了拉普拉斯相关信源的最优解码问题。在1/2码率情况下，当码长为75个256元符号（等效于600个比特）和355个256元符号（等效于2840个比特）时，多元分布式算术码的误帧率只有基于LDPC码的分布式信源编码实现方式的一半左右（图3A和3B），而在曼哈顿残差这一指标上多元分布式算术码的优势甚至更加显著（图3C和3D）。上述工作表明：多元分布式算术码解决了当前基于信道码的分布式信源编码实现方式无法达到理论极限的问题，是实现多个相关信源分布式编码的优良候选方案。
项目研究成果为有效降低多节点信源编码应用场景中的编码端算力需求提供了理论基础和新的解决思路。
鏂囩珷鏉ユ簮国家自然科学基本委员会锛屽垎浜彧涓哄鏈氦娴侊紝濡傛秹鍙婁镜鏉冮棶棰樿鑱旂郴鎴戜滑锛屾垜浠皢鍙婃椂淇敼鎴栧垹闄ゃ
-
2026骞寸浜斿眾鏈哄櫒瀛︿範銆佷簯璁＄畻涓庢櫤 26
-
2026骞寸浜屽眾璁＄畻鏈鸿瑙変笌鏈哄櫒瀛︿範 627
-
2026骞6鏈堜紭璐ㄥ浗闄呭鏈細璁帹鑽 1157
-
2026骞存櫤鎱ф暀鑲蹭笌鏁版嵁鎸栨帢鍥介檯瀛︽湳 813
-
2026骞寸11灞婄敓鐗╁尰瀛︿俊鍙蜂笌鍥惧儚 697
-
2026璧勬簮銆佸寲瀛﹀寲宸ヤ笌搴旂敤鏉愭枡鍥介檯 2559
-
2026骞村浘鍍忓鐞嗕笌鏁板瓧鍒涙剰璁捐鍥介檯 2369
-
2026骞存満姊板伐绋嬶紝鏂拌兘婧愪笌鐢垫皵鎶鏈 6849
-
2026骞存潗鏂欑瀛︺佷綆纰虫妧鏈笌鍔ㄥ姏宸 2524
-
2026骞存捣娲嬬瀛︺佹按鍒╁伐绋嬩笌鐜绠 06-18
-
2026骞寸幆澧冨伐绋嬨佹潗鏂欑瀛︿笌寰幆缁 06-18
-
2026骞磋埅绌哄姩鍔涖佹祦浣撳姏瀛︿笌鐑墿鐞 06-18
-
2026骞村湴鐞冨寲瀛︺佹牳鐗╃悊涓庡湴璐ㄥ鍥 06-18
-
2026骞村井鏈虹數銆佺墿鐞嗗涓庡缓妯′豢鐪熷浗 06-18
-
2026骞存満姊板伐绋嬨佺數瀛愭妧鏈笌鑷姩鍖 06-18
2026骞寸數瀛, 閫氫俊涓庤绠楁満绉戝鍥介檯浼氳 .
绗簲灞婂厛杩涘埗閫犳妧鏈笌鍒堕犵郴缁熷浗闄呭鏈細璁紙I.
绗簩灞婅埅绌鸿埅澶┿佷俊鎭妧鏈笌鎺у埗宸ョ▼鍥介檯瀛︽湳浼.
绗竷灞婄粡娴庣鐞嗕笌澶ф暟鎹簲鐢ㄥ浗闄 瀛︽湳浼氳锛圛.
绗竷灞婂績鐞嗗仴搴蜂笌鏁欒偛銆佷汉鏂囧彂灞曞浗闄呭鏈細璁紙.
2026骞存櫤鑳藉尰瀛﹀拰鍥惧儚璁＄畻鍥介檯浼氳(IMI.
绗叚灞婂厜瀛︽垚鍍忎笌鍥惧儚澶勭悊鍥介檯瀛︽湳浼氳 (IC.
2026骞寸涓冨眾鎺у埗, 鏈哄櫒浜轰笌鏅鸿兘绯荤粺鍥介檯.
绗叚灞婄數瀛愪俊鎭伐绋嬩笌璁＄畻鏈烘妧鏈浗闄呭鏈細璁紙.
绗節灞婅绠楁満淇℃伅绉戝涓庝汉宸ユ櫤鑳藉浗闄呭鏈細璁(.
2026骞存櫤鑳芥満鍣ㄤ汉涓庢帶鍒舵妧鏈浗闄呬細璁(CI.
2026骞翠紶鎰熷櫒鎶鏈佽嚜鍔ㄥ寲涓庢櫤鑳藉埗閫犲浗闄呬細.
绗簩灞婂厛杩涚數瀛愩佹櫤鑳芥妧鏈笌璁＄畻鍥介檯瀛︽湳浼氳锛.
2026骞撮氫俊, 鏁版嵁绉戝涓庢櫤鑳借绠楀浗闄呬細璁.
2026骞寸浜斿眾绠楁硶銆佹暟鎹寲鎺樺拰淇℃伅鎶鏈浗闄.
2026骞翠汉宸ユ櫤鑳戒笌鏈哄櫒浜虹郴缁熷浗闄呬細璁(IC.
2026骞寸浜屽眾鐢靛姏涓庡彲鎸佺画鑳芥簮鎶鏈浗闄呬細璁.
2026IEEE绗笁灞婁簹娲插厛杩涚數姘斾笌鐢靛姏宸ョ▼.
-
2026 JCR褰卞搷鍥犲瓙姝ｅ紡鍙戝竷272
-
涓浗绉戝崗鍙戝竷2025骞淬婇噸瑕佸鏈858
-
2026骞存柊閿愬垎鍖猴紙鍘熶腑绉戦櫌鏈熷垔5648
-
2025骞翠袱闄㈤櫌澹閫夋湁鏁堝欓変汉5280
-
濂藉鏈:绉戠爺缃戝潃瀵艰埅|瀛︽湳澶存潯鍒6842
-
2025骞村浗闄呮湡鍒婇璀﹀悕鍗曞彂甯!7028
-
2025骞翠腑绉戦櫌鏈熷垔鍒嗗尯琛ㄩ噸纾呭彂24788
-
鍚夋灄澶у鏍￠暱寮犲笇锛氬鏈細璁腑鐨勬彁8093
-
鐮旂┒琛ㄦ槑澶槼鑰鏂戠粓绔縺娉㈠彲浣滀负鍦06-24
-
鐮旂┒鎻ず钘烩旇弻鍏辩敓浣撶郴寮哄寲鍏绘畺灏06-24
-
鍙屽姛鑳芥墜鎬у弻鏍搁晬鍌寲鐮旂┒鑾疯繘灞06-24
-
鐮旂┒鍙戠幇閾舵渤绯讳腑蹇冩瀬绔幆澧冧笅澶ц川06-24
-
搴熷鏂欏崌绾у埄鐢ㄧ爺绌跺彇寰楄繘灞06-24
-
纭掑お闃宠兘鐢垫睜鐮旂┒鍙栧緱杩涘睍06-24
-
鍗椾含澶у鐜嬫稕鍥㈤槦棣栨鍙戠幇110浜06-24
-
西南交通大学 23335
-
《临床与转化医学研究》杂志社 2424
-
上海优势商务咨询有限公司 21335
-
梵净山红豆杉开发有限公司 18349
-
成长在北京-线下网站北京发展网 18736
-
湖南红塬文化传播有限公司 21315
-
上海同巨文化传播有限公司 24490
-
西北工业大学无线网络与通信实验室 21709
-
徽州文化园---华商山庄 23379
-
百奥泰国际会议（大连）有限公司 8336
-
数理科学新理论推广中心实践基地 8368
-
中国营养学会 21289
-
金石商务酒店 24260
-
广州市广播电视大学 18334
-
北京嘉城信合汽配贸易有限公司 21450
-
浙江大学创新与发展研究中心 21537
-
中国广东东莞 18445
-
海南国际医药创新联合基金会 8530
-
PPCE 23535
-
中国环境科学学会 24589
